link teman-teman
Kimia (1-5)
aisyahnoer.blogspot.com
pejantantangguh20.blogspot.com
arinimila.blogspot.com
andrechoiru.blogspot.com
desitaevasilawana05.blogspot.com
Fisika (6-10)
ayukusuma8.blogspot.com
dianarist.blogspot.com
elinadwi.blogspot.com
Biologi (11-15)
fatmatri.blogspot.com
kangmasman.blogspot.com
gigihsuryanto13.blogspot.com
rohmaindah.blogspot.com
Matematika (16-20)
safruty.blogspot.com
khoirotunnisak19.blogspot.com
khodiyah.blogspot.com
khusnul1903.blogspot.com
Bahasa Indonesia
lofitasari23.blogspot.com
lilarozzyasih.blogspot.com
lufitanisa.blogspot.com
kikiputrasangpemimpi.blogspot.com
palupi98.blogspot.com
Bahasa Inggris
ceritayazin.blogspot.com
sabtarieka.blogspot.com
riskhilathifah.blogspot.com
vickywulan.blogspot.com
aditn.blogspot.com
zahrakhomar.blogspot.com
riza29.blogspot.com
aisyahnoer.blogspot.com
pejantantangguh20.blogspot.com
arinimila.blogspot.com
andrechoiru.blogspot.com
desitaevasilawana05.blogspot.com
Fisika (6-10)
ayukusuma8.blogspot.com
dianarist.blogspot.com
elinadwi.blogspot.com
Biologi (11-15)
fatmatri.blogspot.com
kangmasman.blogspot.com
gigihsuryanto13.blogspot.com
rohmaindah.blogspot.com
Matematika (16-20)
safruty.blogspot.com
khoirotunnisak19.blogspot.com
khodiyah.blogspot.com
khusnul1903.blogspot.com
Bahasa Indonesia
lofitasari23.blogspot.com
lilarozzyasih.blogspot.com
lufitanisa.blogspot.com
kikiputrasangpemimpi.blogspot.com
palupi98.blogspot.com
Bahasa Inggris
ceritayazin.blogspot.com
sabtarieka.blogspot.com
riskhilathifah.blogspot.com
vickywulan.blogspot.com
aditn.blogspot.com
zahrakhomar.blogspot.com
riza29.blogspot.com
MATRIKS
MATRIKS
Matriks adalah kumpulan bilangan atau unsur yang disusun menurut baris dan kolom. Bilangan-bilangan yang disusun tersebut disebut elemen-elemen atau komponen-komponen matriks. Nama sebuah matriks dinyatakan dengan huruf kapital. Banyak baris x banyak suatu kolom dari suatu matriks disebut ordo matriks.
Secara umum matriks dapat ditulis dengan :

Dalam hal ini aij disebut elemen matriks pada baris ke-i dan kolom ke-j.
2. Beberapa Jenis Matriks
(i) Matriks Nol (0)
Adalah matriks yang semua elemennya bernilai nol.
Adalah matriks yang semua elemennya bernilai nol.
(ii) Matriks bujur sangkar
Adalah matriks yang banyak barisnya sama dengan banyak kolomnya.
(iii) Matriks Bujur sangkar
Adalah matriks yang banyak barisnya sama dengan banyak kolomnya.

(iv) Matriks Diagonal
Adalah matriks bujur sangkar yang semua elemen diluar elemen diagonal utama bernilai nol.

(v) Matriks Identitas
Adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai satu.

(vi) Matriks Segitiga Atas
Adalah matriks bujur sangkar yang elemen-elemen dibawah diagonal utamanya bernilai nol.

(vii) Matriks Segitiga Bawah
Adalah Matriks bujur sangkar yang elemen-elemen diatas diagonal utamanya bernilai nol.

3. Operasi Matriks
- Penjumlahan atau pengurangan matriks
Matriks A dan B dapat dijumlahkan atau dikurangkan jika ordo A = ordo B
 b. Perkalian Matriks dengan Skalar
Jika Skalar dikalikan dengan matriks, maka akan diperoleh sebuah matriks
yang elemen- elemennya merupakan perkalian skalar tersebut dengan
setiap elemen matriks.
b. Perkalian Matriks dengan Skalar
Jika Skalar dikalikan dengan matriks, maka akan diperoleh sebuah matriks
yang elemen- elemennya merupakan perkalian skalar tersebut dengan
setiap elemen matriks. c. Perkalian Dua Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).
4. Transpos Matriks
Transpos dari suatu matriks merupakan pengubahan baris menjadi kolom dan kolom menjadi baris. Tranpos dari matriks A dinotasikan dengan AT atau At.
5. Determinan Matriks
Matriks yang mempunyai determinan hanyalah matriks bujur sangkar (banyaknya baris sama dengan banyaknya kolom).

Limit Fungsi
Limit fungsi.
Limit fungsi adalah salah satu materi yang cukup fundamental untuk mempelajari materi yang lebih tinggi, yaitu tentang kalkulus ( diferensial dan integral).
Sifat-sifat limit fungsi
Limit fungsi mempunyai sifat-sifat sebagai berikut :
Limit fungsi f(x) untuk x => a, a tidak 0.
Pembahasan soal limit fungsi lengkap.
lakukan substitusi, hasilnya sebagai berikut :
Limit fungsi adalah salah satu materi yang cukup fundamental untuk mempelajari materi yang lebih tinggi, yaitu tentang kalkulus ( diferensial dan integral).
Sifat-sifat limit fungsi
Limit fungsi mempunyai sifat-sifat sebagai berikut :
Limit fungsi f(x) untuk x => a, a tidak 0.
Perhitungan limit fungsi f(x) untuk x =>a , a tidak nol, dapat
dilakukan dengan tiga cara, yaitu substitusi langsung, pemfaktoran, dan
rasionalisasi bentuk akar. Jika dengan cara substitusi langsung
dihasilkan dalam bentuk tentu, maka itu hasilnya, tetapi jika dengan
cara substitusi dihasilkan bentuk tak tentu yaitu 0/0, maka perhitungan
limit dilakukan dengan cara pemfaktoran atau rasionalisasi bentuk akar.
Soal dan pembahasan limit fungsi no 1 dan no 2 adalah soal yang
menggunakan substitusi langsung, dan bisa di ketahui nilainya dan untuk
soal no 3 di bawah ini tidak bisa diselesaikan dengan substitusi
langsung, berikut contoh soal limit fungsi yang tidak bisa diselesaikan
dengan substitusi langsung.
Pembahasan soal limit fungsi lengkap.
lakukan substitusi, hasilnya sebagai berikut :
Setelah dilakukan substitusi hasilnya adalah limit dengan hasil bentuk
tak tentu (0/0), maka soal diatas tidak dapat diselesaikan dengan cara
substitusi. Karena limit fungsi tidak dapat diselesaikan dengan
substitusi langsung, makaa langkah selanjutnya adalah dengan cara
memfaktorkan pembilang dan penyebut, sebagai berikut :
Logaritma
Diposting oleh
Unknown
di
23.32
PENGETIAN FUNGSI LOGARITMA.
Fungsi Logaritma adalah fungsi yang peubah bebasnya berupa bentuk logaritma. Fungsi Logaritma adalah Invers dari fungsi eksponen.
Kesetaraan antara sifat-sifat logaritma dan eksponen.
Sifat kesetaraan tersebut dapat melukiskan bahwa grafik fungsi a log x =
y sebagai hasil pencerminan terhadap garis y = x dari grafik fungsi
eksponen y = a (pangkat) x.
Atau Hubungan logaritma dengan eksponen dapat ditulis sebagai berikut :
dengan, a disebut bilangan pokok
b disebut numerus
x disebut hasil logaritma
Bentuk x = a log b dibaca : x adalah logaritma dari b dengan bilangan pokok a. Logaritma dengan bilangan pokok 10 cukup ditulis log saja.
contoh : 10 log 8 cukup ditulis log 8.
adapun untuk mempermudah menyerderhanakan bentuk logaritma terdapat
rumus-rumus, dan berikut adalah rumus untuk menyederhanakan bentuk
logaritma :
statistika
Diposting oleh
Unknown
di
23.03
Pelajaran Statistika di tingkat SMA meliputi mean, modus, median, jangkauan, simpangan, dan ragam
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar.
Selisih antara nilai data terbesar dengan nilai data terkecil.
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
b) Rumus Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
c) Rumus Rataan Hitung Gabungan
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
2. Rumus Modus
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
3. Rumus Median (Nilai Tengah)
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar.
b) Data yang Dikelompokkan
4. Rumus Jangkauan ( J )
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
Selisih antara nilai data terbesar dengan nilai data terkecil.
5. Rumus Simpangan Quartil (Qd)
6. Rumus Simpangan baku ( S )
7. Rumus Simpangan rata – rata (SR)
8. Rumus Ragam (R)
Peluang
Diposting oleh
Unknown
di
22.27
- Kaidah Pencacahan, Permutasi dan Kombinasi
- Kaidah Pencacahan
Apabila peristiwa pertama dapat terjadi dalam p cara berbeda, peristiwa kedua q cara berbeda, peristiwa ketiga r cara berbeda, dan seterusnya, maka banyaknya cara yang berbeda terhadap rangkaian berurutan seperti itu adalah = p x q r x .. - Faktorial
Perkalian n bilangan asli pertama disebut n faktorial, dinotasikan dengan n!
n! = 1 x 2 x 3 x 4 x …. x (n – 1) x n
atau n! = n x (n – 1) x (n – 2) x ….. x 4 x 3 x 2 x 1 - Permutasi
Cara menempatkan n buah unsur ke dalam r tempat yang tersedia dengan urutan diperhatikan disebut permutasi r unsur dari n unsur(r ≤ n) yang dinotasikan dengan nPr atau P(n,r) atau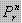 atau Pn,r
atau Pn,r - Banyaknya permutasi n unsur berbeda disusun n unsur(seluruhnya) adalah : P = n!
- Banyaknya Permutasi yang dapat disusun dari n anggota suatu himpunan diambil r unsur anggota pada satu saat adalah :
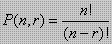
- Banyaknya permutasi jika ada beberapa elemen/unsur yang sama adalah :
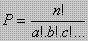
- Banyaknya permutasi siklis adalah permutasi yang disusun secara
melingkar dengan memperhatikan urutannya(arah putarannya) adalah :
P = (n – 1)! - Kombinasi
Cara menempatkan n buah unsur ke dalam r tempat yang tersedia dengan urutan tidak diperhatikan
disebut Kombinasi r unsur dari n unsur(r ≤ n) yang dinotasikan dengan nCr atau C(n,r) atau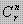 atau Cn,r
atau Cn,r
Kombinasi n unsur berbeda disusun r unsur dirumuskan :
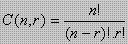
- Binomial Newton
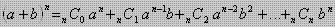
- Kaidah Pencacahan
- Peluang Suatu Kejadian
- Dalam suatu percobaan :
- Semua hasil yang mungkin disebut ruang sampel
- Setiap anggota dalam ruang sampel disebut titik sampel
- Hasil yang diharapkan disebut kejadian
- Definisi Peluang
Peluang kejadian A dinotasikan dengan P(A) adalah perbandingan banyaknya hasil kejadian A dinotasikan n(A)
terhadap banyaknya semua hasil yang mungkin dinotasikan dengan n(S) dalam suatu percobaan.
Kisaran nilai peluang suatu kejadian A adalah 0 ≤ P(A) ≤ 1.
Jika P(A) = 0 disebut kemustahilan dan P(A) = 1 disebut kepastian - Frekuensi Harapan
Frekuensi Harapan kejadian A adalah banyaknya kejadian A yang diharapkan dalam beberapa kali percobaan
Jika percobaan dilakukan sebanyak n kali maka frekuensi harapan kejadian A dirumuskan : Fh(A) = n x P(A) - Peluang Komplemen Suatu Kejadian
Jika Ac kejadian selain A, maka P(A)c = 1 – P(A) atau
P(A)c + P(A) = 1
P(A)c = peluang komplemen kejadian A atau peluang kejadian selain kejadian A - Kejadian Majemuk
- Untuk sembarang kejadian A atau B berlaku :
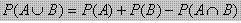
- Peluang dua Kejadian saling lepas(asing)
Jika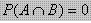 maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
Besarnya peluang dua kejadian saling lepas(asing) adalah :
- Peluang dua kejadian saling bebas
Bila kejadian A tidak mempengaruhi terjadinya B dan sebaliknya, maka kejadian semacam ini disebut dua kejadian saling bebas
Peluang dua kejadian saling bebas dirumuskan :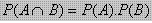
- Peluang dua kejadian tak bebas(bersyarat/bergantungan)
Apabila kejadian kedua(B) adalah kejadian setelah terjadinya kejadian pertama A, dinotasikan (B/A),
maka dua kejadian tersebut merupakan dua kejadian tak bebas(bersyarat)
Peluang dua kejadian tak bebas dirumuskan :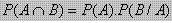
program linier
Diposting oleh
Unknown
di
22.15
Program linear yaitu suatu metode untuk mencari nilai maksimum atau nilai minimum dari bentuk linear pada daerah yang dibatasi grafik -grafik fungsi linear.
Selanjutnya arsir daerah yang memenuhi persamaan, seperti gambar dibawah ini.
Himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah merupakan suatu himpunan titik-titik (pasangan berurut (x,y)) dalam bidang cartesius yang memenuhi semua pertidaksamaan linear dalam sistem tersebut. Sehingga daerah himpunan penyelesaiannya merupakan irisan himpunan-himpunan penyelesaian dari pertidaksamaan dalam sistem pertidaksamaan linear dua peubah itu. Untuk lebih mudah dalam memahami daerah penyelesaian dari sistem pertidak-samaan linear dua peubah, perhatikan contoh berikut.
Selanjutnya arsir daerah yang memenuhi persamaan, seperti gambar dibawah ini.
Daerah penyelesaian sistem pertidaksamaan merupakan irisan dari ketiga himpunan penyelesaian pertidaksamaan di atas, yaitu seperti terlihat pada gambar berikut ini (daerah yang diarsir).
Pertidaksamaan Linear juga dapat digunakan untuk memecahkan masalah dalam kehidupan sehari-hari. Hal ini dapat dilakukan dengan memodelkan masalah menjadi model matematika. Jadi, Model matematika merupakan suatu cara sederhana untuk menerjemahkan suatu masalah ke dalam bahasa matematika dengan menggunakan persamaan, pertidaksamaan, atau fungsi.
LOGIKA
LOGIKA MATEMATIKA
A. Negasi (Ingkaran)
Negasi
adalah pengingkaran terhadap nilai kebenaran suatu pernyataan. ~ p : tidak p
p
|
~ p
|
B
|
S
|
S
|
B
|
B. Operator Logika
1)
Konjungsi adalah
penggabungan dua pernyataan atau lebih dengan operator “dan”.
p Ù
q : p dan q
2)
Disjungsi adalah
penggabungan dua pernyataan atau lebih dengan operator “atau”.
p Ú
q : p atau q
3) Implikasi
adalah penggabungan dua pernyataan dengan operator “Jika …, maka …”.
p Þ
q : Jika p maka q
4)
Biimplikasi adalah penggabungan dua pernyataan dengan operator “… jika
dan hanya jika …”
p Û q :
p jika dan hanya jika q
C. Nilai Kebenaran Konjungsi, Disjungsi,
Implikasi, dan Biimplikasi
premis 1
|
premis 2
|
konjungsi
|
disjungsi
|
implikasi
|
biimplikasi
|
P
|
q
|
P Ù q
|
p Ú q
|
p Þ q
|
p Û q
|
B
|
B
|
B
|
B
|
B
|
B
|
B
|
S
|
S
|
B
|
S
|
S
|
S
|
B
|
S
|
B
|
B
|
S
|
S
|
S
|
S
|
S
|
B
|
B
|
Kesimpulan:
perhatikan nilai kebenaran yang tercetak tebal
1) Konjungsi akan bernilai benar (B), jika kedua premis benar,
2) Disjungsi akan bernilai salah (S), jika kedua premis salah
3) Implikasi akan bernilai salah (S), jika premis
sebelah kiri benar (B) dan kanan
salah (S)
4) Biimimplikasi akan bernilai benar (B),
jika premis kiri dan kanan
kembar
D. Konvers,
Invers, dan Kontraposisi
Bila terdapat bentuk implikasi p Þ q,
maka diperoleh tiga pengembangannya sebagai berikut:
Implikasi
|
Invers
|
Konvers
|
Kontraposisi
|
p Þ q
|
~ p Þ ~
q
|
q Þ p
|
~ q Þ ~
p
|
Kesimpulan yang dapat diambil adalah:
1) invers adalah negasi dari implikasi
2) konvers adalah kebalikan dari implikasi
3) kontraposisi adalah implikasi yang
dibalik dan dinegasi
E. Pernyataan-Pernyataan
yang Equivalen
1)
implikasi º kontraposisi : p Þ q º ~ q Þ ~ p
2)
konvers º invers : q Þ p º ~ p Þ ~ q
3)
~(p Ù q) º ~ p Ú ~ q : ingkaran dari konjungsi
4)
~(p Ú q) º ~ p Ù ~ q :
ingkaran dari disjungsi
5)
~(p Þ q) º p Ù ~ q :
ingkaran dari implikasi
6)
p Þ q º ~ p Ú q
7)
~(p Û q) º (p Ù ~ q) Ú (q Ù ~ p) : ingkaran dari
biimplikasi
F. Kuantor Universal dan Kuantor Eksistensial
- Kuantor Universal adalah suatu pernyataan yang berlaku untuk umum, notasinya “"x” dibaca “untuk semua nilai x”
- Kuantor Eksistensial adalah suatu pernyataan yang berlaku secara khusus, notasinya “$x” dibaca “ada nilai x” atau “beberapa nilai x”
- Ingkaran dari pernyataan berkuantor
1) ~("x) º $(~x)
2) ~($x) º "(~x)
G. Penarikan
Kesimpulan
Jenis
penarikan kesimpulan ada 3 yaitu:
1) Modus Ponens 2) Modus Tollens 3) Silogisme
(MP) (MT)
p Þ q
|
: premis 1
|
p Þ q
|
: premis 1
|
p Þ q
|
: premis 1
|
p
|
: premis 2
|
~q
|
: premis 2
|
q Þ r
|
: premis 2
|
\q
|
: kesimpulan
|
\~p
|
: kesimpulan
|
\p Þ r
|
: kesimpulan
|
Langganan:
Komentar (Atom)























